Linear Wave 방정식#

강좌: 기초 전산유체역학

선형 파동 방정식#

1차원 선형 파동 방정식은 다음과 같다.

\[ \frac{\partial u}{\partial t} + a \frac{\partial u}{\partial x} = 0. \]

여기서 상수 \(a\) 는 파의 전파속도이다. 다음 초기 조건에 의한 완전해는

\[ u(x,0) = F(x),~~~-\infty < x < \infty \]

아래와 같다.

\[ u(x,t) = F(x-at). \]

유한차분법#

\(n\) 번째 시간 \(t^n\), \(j\) 번째 격자점 \(x_j\) 에서 근사해를 다음과 같이 표현하자.

\[ u_j^n = u(x_j, t^n). \]

First approach (Central difference)#

시간에 대한 차분은 우선 Euler Explicit 방법을 생각하자.

\[ \frac{\partial u}{\partial t} \approx \frac{u_j^{n+1} - u_{j}^n}{\Delta t}. \]

공간에 대한 차분은 중앙차분을 생각하자.

\[ a \frac{\partial u}{\partial x} \approx a \frac{u_{j+1}^n - u_{j-1}^n}{2 \Delta x} \]

이를 정리하면 다음 기법을 만들 수 있다.

\[ u_j^{n+1} = u_{j}^n - \frac{a \Delta t}{2 \Delta x} (u_{j+1}^n - u_{j-1}^n). \]

Second approach (Upwind difference)#

\(a>0\) 인 경우 공간에 대한 차분을 1차 backward difference로 생각하자.

\[ a \frac{\partial u}{\partial x} \approx a \frac{u_{j}^n - u_{j-1}^n}{\Delta x} \]

이를 정리하면 다음 기법을 만들 수 있다.

\[ u_j^{n+1} = u_{j}^n - \frac{a \Delta t}{\Delta x} (u_{j}^n - u_{j-1}^n). \]

Sine wave 예제#

계산 영역은 \(x \in [-1, 1]\) 이고 초기 조건은 다음과 같다.

\[ u(x,0) = \sin(\pi x) \]

양 끝점에서 경계 조건은 Periodic 조건을 주자. 수식적으로는

\[ u(-1, t) = u(1, t). \]

시간 \(t=1.5\) 일 때 해를 구하자.

계산 격자 구성, Solution array 구성#

계산 영역을 \(n_x + 1\)개의 점으로 나누어보자.

즉 격자점은 다음과 같다.

\[ x_j = -1, -1 + \Delta x, -1 + 2 \Delta x, ..., 1 - \Delta x, 1 ~~(1 \le j \le n_x +1) \]

첫번째 격자점을 계산하기 위해서는 \(x_0 = -1 - \Delta x\) 값이 필요하다. 또한 마지막 격자점을 계산하기 위해서는 \(x_{n_x+2} = 1 + \Delta x\) 값이 필요하다.

이를 대칭조건으로 구현하면 다음과 같다.

\[\begin{split} u_0^n = u_{n_x}^n \\ u_{n_x+2}^n = u_2^n \end{split}\]

경계 조건을 위해서 Solution array는 격자점 + 2개의 경계 조건을 고려해서 \(n_x+3\) 으로 구성한다.

시간 간격은 \(\Delta t = 0.01\) 에 대해서 \(n_x=50\) 인 경우 계산하면 다음과 같다.

from matplotlib import pyplot as plt

import numpy as np

plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150

def central(nx, u, dt, dx, a, du):
    """
    Central difference

    Parameters
    ----------
    nx : integer
        등분 개수
    u : array
        Solution
    dt : float
        시간간격
    dx : float
        격자 간격
    a : float
        Wave speed
    du : array
        증가량
    """
    for i in range(1, nx+2):
        du[i] = -0.5*a*(u[i+1] - u[i-1])/dx*dt

def central_v1(u, dt, dx, a):
    """
    Central difference (vector version)

    Parameters
    ----------
    u : array
        Solution
    dt : float
        시간간격
    dx : float
        격자 간격
    a : float
        Wave speed

    Return
    ------
    du : array
        증가량
    """
    # Size of u : nx + 3
    # 0, nx+2 (or -1) - ghost cell, 
    # 1 - nx+1 (or -2) - Inner
    return -0.5*a*(u[2:] - u[:-2])/dx*dt

def bc_periodic(u):
    """
    Boundary condition (peridoic)

    Parameter
    ---------
    u : array
        solution
    """
    # index (nx : -3), (nx+2 : -1)
    u[0] = u[-3]
    u[-1] = u[2]

# Constants
a = 1.0

nx = 50
dt = 0.01
t_target = 1.5

# Make grid
x = np.linspace(-1, 1, nx+1)
dx = np.diff(x)[0]

# Solution array
u = np.empty(nx+3)
du = np.zeros_like(u)

# Initialize
u[1:-1] = np.sin(np.pi*x)
bc_periodic(u)

# Calculation
t = 0
while abs(t - t_target) > 1e-8:
    # Adjust time step to reach target time
    dt = min(dt, t_target - t)
    
    # Periodic BC
    bc_periodic(u)
    
    # Scheme
    #du[1:-1] = central_v1(u, dt, dx, a)
    central(nx, u, dt, dx, a, du)
    
    # Update
    u += du
    t += dt
    
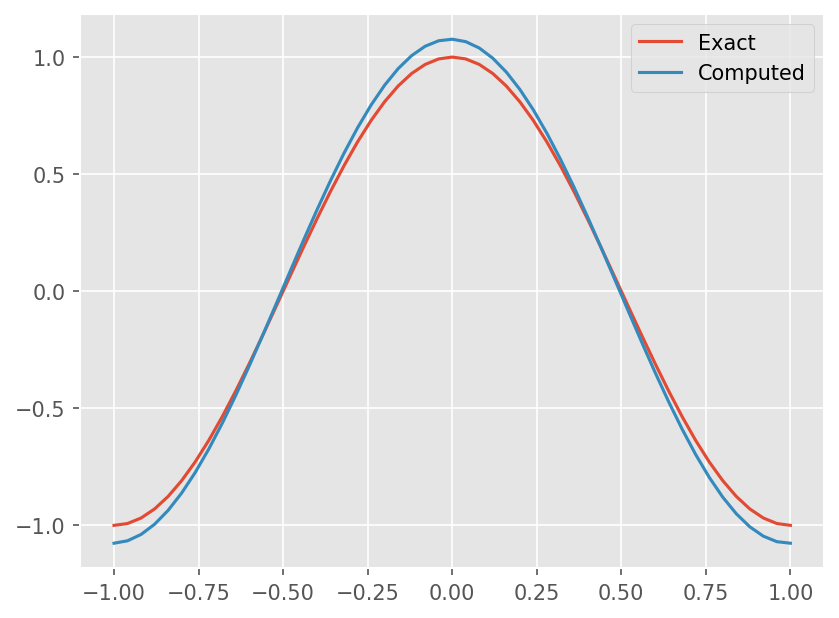
# Compare with exact solution
u_exact = np.sin(np.pi*(x-a*t))
plt.plot(x, u_exact)
plt.plot(x, u[1:-1])
plt.legend(['Exact', 'Computed'])

<matplotlib.legend.Legend at 0xff3314c95d00>

../_images/1d989cc7c4b0fe61a644173378434d6e52cb12fafbcce2411fa8b3c874183f24.png

실습#

Central 기법에 대해 격자 개수와 시간 간격을 아래와 같이 달리하면셔 결과를 비교하시오.
- \(N\) = 50, 100, 200
- \(\Delta t = 0.005, 0.01, 0.02, 0.05, 0.1\)
Upwind difference를 구현한 후, Sine Wave 문제를 해석하시오. Central 기법과 결과 차이를 비교하시오.
다음 Square Wave에 대해 Central difference 와 Upwind difference를 해석하시오.

\[\begin{split} u(x,0) = \begin{cases} 0, & \text{if } x < -0.25 \\ 1, & \text{if } -0.25 \leq x < 0.25 \\ 0, & \text{if } x > 0.25 \end{cases} \end{split}\]

(Optional) \(a < 0\) 일때 Upwind difference 기법은 공간에 대해 Forward 차분식을 적용해야 한다. \(a=-1\)인 경우에 대해 Upwind 기법을 구현하시오.

Linear Wave 방정식

Contents